KARNATAKA - SSLC - MATHMATICS - QUESTION PAPER - APRIL 2017 - WITH Hints/Answer Keys

General Instructions to the Candidate
1. This Question Paper consists of 40 objective and subjective types of questions.
2. This question paper has been sealed by the reverse jacket. You have to cut on the right side to open the paper at the time of commencement of the examination. Check whether all the pages of the question paper are intact.
3. Follow the instructions given against both the objective and subjective types of questions.
4. Figures in the right hand margin indicate maximum marks for the questions.
5. The maximum time to answer the paper is given at the top of the question paper. It includes 15 minutes for reading the question paper.
Correction only in this paper : In equations please consider superscripts. ex. take r2 as r square.
I. Four alternatives are given for each of the following questions / incomplete statements. Only one of them is correct or most appropriate. Choose the correct alternative and write the complete answer along with its letter of alphabet 8 × 1 = 8
1. If a polynomial p ( x ) = x2 – 4 is divided by a linear polynomial ( x – 2 ) then the remainder is
(A) 2
(B) – 2
(C) 0
(D) – 8.
2. The sum and product of the roots of the equation x2 + 2x + 1 = 0 are respectively :
(A) 2 and – 1
(B) – 2 and 1
(C) – 2 and – 1
(D) 1 and 2.
3. In a circle the angle between a radius and a tangent at non-center end of the radius is
A) 90°
(B) 180°
(C) 45°
(D) 360°
4. The volume of a right circular cylinder whose circular base area is 154 sq.cm and height 10 cm is
(A) 15·40 c.c.
(B) 15400 c.c.
(C) 1·540 c.c.
(D) 1540 c.c.
5. If tanθ = 1/√3 and cos θ = √3/2 then the value of sin θ is
√3
½
2/√3
3/2
6. ( 7 × 11 × 13 + 13 ) is a / an
(A) Composite number
(B) Prime number
(C) Irrational number
(D) Imaginary number.
7. The sum of an infinite geometric series whose first term is a and common ratio is r is given by
S∞ = 1/(a-r)
S∞ = 1/(r-a)
S∞ = a/(1-r)
S∞ = (1-r)/a
Hints :
15. A I B ) I C = { } or φ = A I ( B I C )
16. Let a and b be two numbers and given (a+b)/2 = 5
Or
G2 = AH
17. i.e. 5 – 3 = p/ q where p, q ∈ z, q ≠ 0 S.T (5q-p)/q = √3
18. n ( n – 1 ) ( n – 2 ) ( n – 3 ) = 5n ( n – 1 ) ( n – 2 )
19. P(A)/P(A bar) = 5/11 and P(A bar) = 1 - P(A)
20. A group of surds having the same order and same radicand in their simplest form are called like surds.
A group of surds having different orders or different radicands or both in their simplest form are called unlike surds.
Set of like surds — c) { √8 , √18 , √32 , √50 }.
21. : solve : (√5+√3)/(√5-√3) x : (√5+√3)/(√5+√3)
22. Let g ( x ) be divisor = 2x – 1, q ( x ) be quotient = 7x + x + 5 & r ( x ) be remainder = 4 ∴ p ( x ) = [ g ( x ) . q ( x ) ] + r ( x )

23. Find ‘a’ then perimeter triangle is = 3a
24. ST. b2 – 4ac < 0
25. ∴ Δ PXQ ~ Δ ZXY so slopes also nearly same
26. tan2A = sin2A/cos2A
27. Slope = (y2-y1)/(x2-x1)
28. Mid-point = {(x1+x2)/2 , (y1+y2)/2
29.

30

________________________________________________________________________________________________
I. Four alternatives are given for each of the following questions / incomplete statements. Only one of them is correct or most appropriate. Choose the correct alternative and write the complete answer along with its letter of alphabet 8 × 1 = 8
1. If a polynomial p ( x ) = x2 – 4 is divided by a linear polynomial ( x – 2 ) then the remainder is
(A) 2
(B) – 2
(C) 0
(D) – 8.
2. The sum and product of the roots of the equation x2 + 2x + 1 = 0 are respectively :
(A) 2 and – 1
(B) – 2 and 1
(C) – 2 and – 1
(D) 1 and 2.
3. In a circle the angle between a radius and a tangent at non-center end of the radius is
A) 90°
(B) 180°
(C) 45°
(D) 360°
4. The volume of a right circular cylinder whose circular base area is 154 sq.cm and height 10 cm is
(A) 15·40 c.c.
(B) 15400 c.c.
(C) 1·540 c.c.
(D) 1540 c.c.
5. If tanθ = 1/√3 and cos θ = √3/2 then the value of sin θ is
√3
½
2/√3
3/2
6. ( 7 × 11 × 13 + 13 ) is a / an
(A) Composite number
(B) Prime number
(C) Irrational number
(D) Imaginary number.
7. The sum of an infinite geometric series whose first term is a and common ratio is r is given by
S∞ = 1/(a-r)
S∞ = 1/(r-a)
S∞ = a/(1-r)
S∞ = (1-r)/a
8. Lateral surface area of the frustum of a cone is

(A) π ( r2 − r1 )h
(B) π ( r1 + r2 )h
(C) π ( r1 − r2 ) l
(D) π ( r1 + r2 ) l
(A) π ( r2 − r1 )h
(B) π ( r1 + r2 )h
(C) π ( r1 − r2 ) l
(D) π ( r1 + r2 ) l
Answers
1. C 0
2. B – 2 and 1
3. A 90°
4. D 1540 c.c.
5. B ½
6. A Composite number
7. C. S∞ = a/(1-r)
8. D. (D) π ( r1 + r2 ) l
________________________________________________________________________________________________
II. Answer the following :
9. If U = { 1, 2, 3, 4, 5, 6 } and A = { 2, 3, 4, 5 } then find Al .
10. Write the relation between the standard deviation of a set of scores and its variance.
11. In a sequence if Tn = n2 + 4 then find T2 .
12. A fair coin is tossed once. Find the probability that head occurs.
13. State Pythagoras theorem.
14. Write the general form of a quadratic polynomial.
Hints :
9. Al = U – A
10. Standard deviation = √varience or SD2 = varience
11. Tn = n2 + 4
12. Sample space ( S ) = { H, T } ∴ n ( S ) = 2 & Event ( A ) = { H } ∴ n ( A ) = 1
P ( A ) = n(A)/ n(S) = ½
13. 13. “In a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on other two sides.”
14. General form p ( x ) = ax2 + bx + c where a ≠ 0, a, b & c ∈R.
________________________________________________________________________________________________
III.
15. Given A = { 1, 2, 3, 4 }, B = { 3, 4, 5, 6 } and C = { 6, 7 }. Verify that ( A ⋂ B ) ⋂ C = A ⋂ ( B ⋂ C ).
16. Arithmetic mean between two numbers is 5 and Geometric mean between them is 4. Find the Harmonic mean between the numbers.
OR
In a harmonic progression third term and fifth terms are respectively 1 and 1/(-5) . Find the tenth term.
17. Prove that 5 – 3 is an irrational number.
18. Find the value of n if nP4 = 5 ( nP3 ).
19. If A is an event in a random experiment such that P ( A ) : P ( A bar ) = 5 : 11, then find P ( A ) and P ( A bar ) .
20. What are like surds and unlike surds ? Identify and write the set of like surds in the following groups :
a) { √8 , √12 , √20 , √54 }
b) { √50 , 3√54 , 4√32 }
c) { √8 , √18 , √32 , √50 }.
21. Rationalise the denominator and simplify : (√5+√3)/(√5-√3)
22. A polynomial p ( x ) is divided by ( 2x – 1 ). The quotient and remainder obtained are ( 7x2 + x + 5 ) and 4 respectively. Find p ( x ).
OR
Find the quotient and remainder using synthetic division. ( 3x3 − 2x2 + 7x − 5 ) ÷ ( x + 3 ).
23. Area of an equilateral triangle is given by A = (√3)a2 /4 where A is the area
and a is the side. Find the perimeter of the triangle if A = 16√3 sq.cm.
24. Show that the roots of the equation x2 – 2x + 3 = 0 are imaginary.
25. In 📐XYZ, P is any point on XY and PQ ⊥ XZ. If XP = 4 cm, XY = 16 cm and XZ = 24 cm, find XQ.
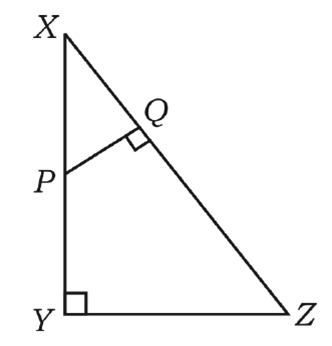
26. Show that (1-tan2A)/(1-tan2A) = 2xos2A-1
27. Find the slope of the line joining the points ( 4, – 8 ) and ( 5, – 2 ).
28. Find the coordinates of the midpoint of the line joining the points ( 2, 3 ) and ( 4, 7 ).
29. Draw a plan of a level ground using the information given below : [ Scale : 20 metres = 1 cm ]
30. Draw a circle of radius 3·5 cm and construct a chord of length 6 cm in it. Measure and write the distance between the centre and the chord.
1. C 0
2. B – 2 and 1
3. A 90°
4. D 1540 c.c.
5. B ½
6. A Composite number
7. C. S∞ = a/(1-r)
8. D. (D) π ( r1 + r2 ) l
________________________________________________________________________________________________
II. Answer the following :
9. If U = { 1, 2, 3, 4, 5, 6 } and A = { 2, 3, 4, 5 } then find Al .
10. Write the relation between the standard deviation of a set of scores and its variance.
11. In a sequence if Tn = n2 + 4 then find T2 .
12. A fair coin is tossed once. Find the probability that head occurs.
13. State Pythagoras theorem.
14. Write the general form of a quadratic polynomial.
Hints :
9. Al = U – A
10. Standard deviation = √varience or SD2 = varience
11. Tn = n2 + 4
12. Sample space ( S ) = { H, T } ∴ n ( S ) = 2 & Event ( A ) = { H } ∴ n ( A ) = 1
P ( A ) = n(A)/ n(S) = ½
13. 13. “In a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on other two sides.”
14. General form p ( x ) = ax2 + bx + c where a ≠ 0, a, b & c ∈R.
________________________________________________________________________________________________
III.
15. Given A = { 1, 2, 3, 4 }, B = { 3, 4, 5, 6 } and C = { 6, 7 }. Verify that ( A ⋂ B ) ⋂ C = A ⋂ ( B ⋂ C ).
16. Arithmetic mean between two numbers is 5 and Geometric mean between them is 4. Find the Harmonic mean between the numbers.
OR
In a harmonic progression third term and fifth terms are respectively 1 and 1/(-5) . Find the tenth term.
17. Prove that 5 – 3 is an irrational number.
18. Find the value of n if nP4 = 5 ( nP3 ).
19. If A is an event in a random experiment such that P ( A ) : P ( A bar ) = 5 : 11, then find P ( A ) and P ( A bar ) .
20. What are like surds and unlike surds ? Identify and write the set of like surds in the following groups :
a) { √8 , √12 , √20 , √54 }
b) { √50 , 3√54 , 4√32 }
c) { √8 , √18 , √32 , √50 }.
21. Rationalise the denominator and simplify : (√5+√3)/(√5-√3)
22. A polynomial p ( x ) is divided by ( 2x – 1 ). The quotient and remainder obtained are ( 7x2 + x + 5 ) and 4 respectively. Find p ( x ).
OR
Find the quotient and remainder using synthetic division. ( 3x3 − 2x2 + 7x − 5 ) ÷ ( x + 3 ).
23. Area of an equilateral triangle is given by A = (√3)a2 /4 where A is the area
and a is the side. Find the perimeter of the triangle if A = 16√3 sq.cm.
24. Show that the roots of the equation x2 – 2x + 3 = 0 are imaginary.
25. In 📐XYZ, P is any point on XY and PQ ⊥ XZ. If XP = 4 cm, XY = 16 cm and XZ = 24 cm, find XQ.
26. Show that (1-tan2A)/(1-tan2A) = 2xos2A-1
27. Find the slope of the line joining the points ( 4, – 8 ) and ( 5, – 2 ).
28. Find the coordinates of the midpoint of the line joining the points ( 2, 3 ) and ( 4, 7 ).
29. Draw a plan of a level ground using the information given below : [ Scale : 20 metres = 1 cm ]
To D (in metres)
| ||
150
| ||
100
|
70 to C
| |
80 to E
|
80
| |
30
|
40 to B
| |
From A
|
30. Draw a circle of radius 3·5 cm and construct a chord of length 6 cm in it. Measure and write the distance between the centre and the chord.
Hints :
15. A I B ) I C = { } or φ = A I ( B I C )
16. Let a and b be two numbers and given (a+b)/2 = 5
Or
G2 = AH
17. i.e. 5 – 3 = p/ q where p, q ∈ z, q ≠ 0 S.T (5q-p)/q = √3
18. n ( n – 1 ) ( n – 2 ) ( n – 3 ) = 5n ( n – 1 ) ( n – 2 )
19. P(A)/P(A bar) = 5/11 and P(A bar) = 1 - P(A)
20. A group of surds having the same order and same radicand in their simplest form are called like surds.
A group of surds having different orders or different radicands or both in their simplest form are called unlike surds.
Set of like surds — c) { √8 , √18 , √32 , √50 }.
21. : solve : (√5+√3)/(√5-√3) x : (√5+√3)/(√5+√3)
22. Let g ( x ) be divisor = 2x – 1, q ( x ) be quotient = 7x + x + 5 & r ( x ) be remainder = 4 ∴ p ( x ) = [ g ( x ) . q ( x ) ] + r ( x )
23. Find ‘a’ then perimeter triangle is = 3a
24. ST. b2 – 4ac < 0
25. ∴ Δ PXQ ~ Δ ZXY so slopes also nearly same
26. tan2A = sin2A/cos2A
27. Slope = (y2-y1)/(x2-x1)
28. Mid-point = {(x1+x2)/2 , (y1+y2)/2
29.
30
________________________________________________________________________________________________
VI.
31. Everybody in a function shakes hand with everybody else. The total number of handshakes are 45. Find the number of persons in the function
OR
Show that the number of diagonals in a polygon of n sides is n(n-3)/2
32. Calculate the coefficient of variation ( C.V. ) of the following data :
40, 36, 64, 48, 52.
33. If two circles touch each other externally, prove that the centres and the point of contact are collinear.
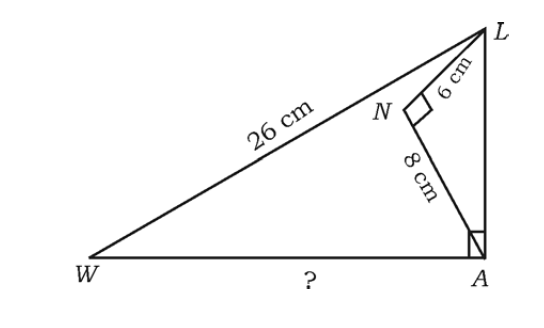
34. In 📐LAW, LAW = 90°, LNA = 90°, LW = 26 cm, LN = 6 cm and AN = 8 cm. Calculate the length of WA.
OR
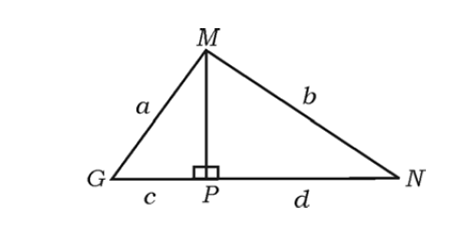
In Δ MGN, MP ⊥ GN. If MG = a units, MN = b units, GP = c units and PN = d units, prove that (a-b)/(c-d) = (c+d)/(a+b)
35. The angle of elevation of the top of a flag post ( AB ) from a point ( C ) on a horizontal ground is found to be 30°. On walking 6 m towards the post at X, the angle of elevation is found to be 60° as shown in the figure. Find the height of the flag post.

OR
Prove that
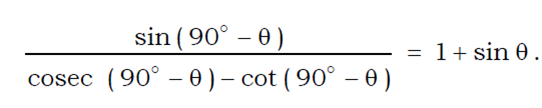
36. A toy is in the form of a cone mounted on a hemisphere as shown in the figure. If the radius of each of these solids is 7/2 cm and height of the cone is 5 cm, find the volume of the toy.
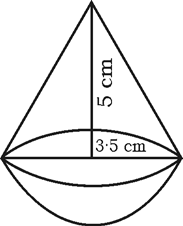
OR
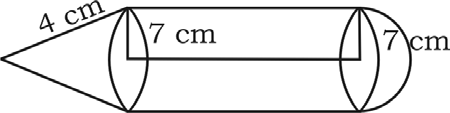
A solid is composed of a cylinder with a hemisphere at one end and a cone at other end as shown in the figure. If the radius of each of these solids is 7 cm and height of the cylinder is equal to slant height of the cone, find the total surface area of the solid if slant height is 4 cm.
Hints :31. nC2 = 45 ( given ) no. of diagonals = nC2 − n
32. Standard deviation ( σ ) = √(∑d2/N)
Coefficient of variation ( C.V. ) = σ/X bar x 100
33. S. T APB is a straight line

34. LA2 = LN2 + NA2 & LW2 = LA2 +WA2
OR
∴ MG2 = MP2 + GP2
∴ MN2 = MP2 + PN2
35.Find hight of AB using tan300 & tan600 equate both to get BX then find AB
OR
sin ( 90° – θ ) = cos θ, cosec ( 90° – θ ) = sec θ, cot ( 90° – θ ) = tan θ
36. Volume of the toy = Volume of the cone + Volume of the hemi-sphere
= ⅓ πr2h+⅔ π r3
T.S.A = πrl + 2πrh + 2πr2
__________________________________________________________________________________________________
31. Everybody in a function shakes hand with everybody else. The total number of handshakes are 45. Find the number of persons in the function
OR
Show that the number of diagonals in a polygon of n sides is n(n-3)/2
32. Calculate the coefficient of variation ( C.V. ) of the following data :
40, 36, 64, 48, 52.
33. If two circles touch each other externally, prove that the centres and the point of contact are collinear.
34. In 📐LAW, LAW = 90°, LNA = 90°, LW = 26 cm, LN = 6 cm and AN = 8 cm. Calculate the length of WA.
OR
In Δ MGN, MP ⊥ GN. If MG = a units, MN = b units, GP = c units and PN = d units, prove that (a-b)/(c-d) = (c+d)/(a+b)
35. The angle of elevation of the top of a flag post ( AB ) from a point ( C ) on a horizontal ground is found to be 30°. On walking 6 m towards the post at X, the angle of elevation is found to be 60° as shown in the figure. Find the height of the flag post.
OR
Prove that
36. A toy is in the form of a cone mounted on a hemisphere as shown in the figure. If the radius of each of these solids is 7/2 cm and height of the cone is 5 cm, find the volume of the toy.
OR
A solid is composed of a cylinder with a hemisphere at one end and a cone at other end as shown in the figure. If the radius of each of these solids is 7 cm and height of the cylinder is equal to slant height of the cone, find the total surface area of the solid if slant height is 4 cm.
Hints :31. nC2 = 45 ( given ) no. of diagonals = nC2 − n
32. Standard deviation ( σ ) = √(∑d2/N)
Coefficient of variation ( C.V. ) = σ/X bar x 100
33. S. T APB is a straight line
34. LA2 = LN2 + NA2 & LW2 = LA2 +WA2
OR
∴ MG2 = MP2 + GP2
∴ MN2 = MP2 + PN2
35.Find hight of AB using tan300 & tan600 equate both to get BX then find AB
OR
sin ( 90° – θ ) = cos θ, cosec ( 90° – θ ) = sec θ, cot ( 90° – θ ) = tan θ
36. Volume of the toy = Volume of the cone + Volume of the hemi-sphere
= ⅓ πr2h+⅔ π r3
T.S.A = πrl + 2πrh + 2πr2
__________________________________________________________________________________________________
V.
37. Construct two circles of radii 4 cm and 2 cm whose centres are 8 cm apart. Construct a transverse common tangent. Measure and write its length.
38. State and prove Basic proportionality ( Thales ) theorem.
39. The third term of a geometric progression is square of its first term and the fifth term of it is 64. Find the sum of the first six terms of the Geometric Progression.
OR
The fourth term of an Arithmetic progression is 10 and the eleventh term of it exceeds three times the fourth term by 1. Find the sum of the first 20 terms of the progression.
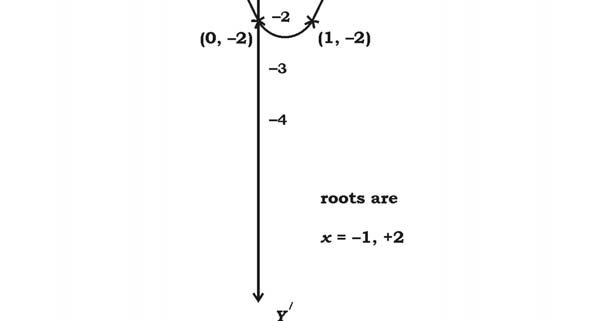
40. Solve the quadratic equation x2 – x – 2 = 0 graphically.
Hints :
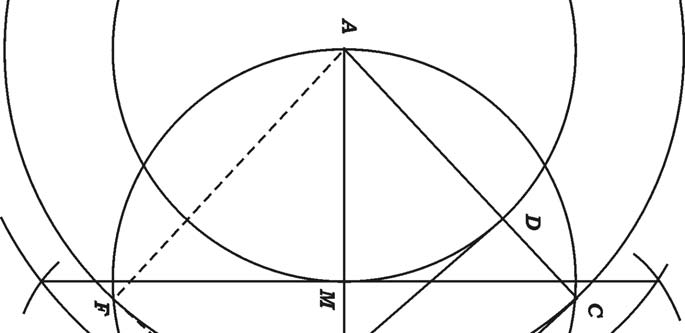

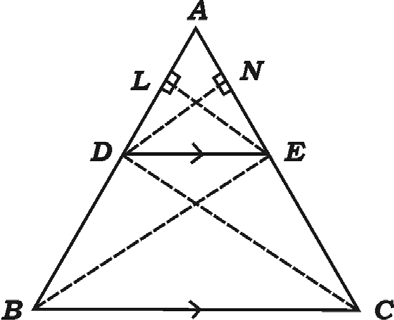
38. Thales theorem or Basic Proportionality theorem. “If a straight line is drawn parallel to a side of a triangle, then it divides the other two sides proportionally.”
39. r2 = a & ar4 = 64 ∴ r = 2
Sn = a(rn-1)/ (r-1)
a + 3d = 10 ∴ d = 3 ∴ a = 10 – 9 = 1
Sn = n/2 [2a+ (n-1)d] = 590
40.


For more comfort can watch videos:
37. Construct two circles of radii 4 cm and 2 cm whose centres are 8 cm apart. Construct a transverse common tangent. Measure and write its length.
38. State and prove Basic proportionality ( Thales ) theorem.
39. The third term of a geometric progression is square of its first term and the fifth term of it is 64. Find the sum of the first six terms of the Geometric Progression.
OR
The fourth term of an Arithmetic progression is 10 and the eleventh term of it exceeds three times the fourth term by 1. Find the sum of the first 20 terms of the progression.
40. Solve the quadratic equation x2 – x – 2 = 0 graphically.
Hints :
38. Thales theorem or Basic Proportionality theorem. “If a straight line is drawn parallel to a side of a triangle, then it divides the other two sides proportionally.”
39. r2 = a & ar4 = 64 ∴ r = 2
Sn = a(rn-1)/ (r-1)
a + 3d = 10 ∴ d = 3 ∴ a = 10 – 9 = 1
Sn = n/2 [2a+ (n-1)d] = 590
40.
For more comfort can watch videos:


No comments: